The Cross-entropy of Piecewise Linear Probability Density Functions
The title of this paper really is a complete summary of what it's about!
But that does hide just how much went into this: it's 31 pages with 218 numbered equations and an average citation year of 1982 (before I was born… just). Or, to put it more directly, the cross entropy (also, KL-divergence and entropy) of piecewise linear functions turns out to be a lot more work than you initially think it's going to be. Was surprised to discover nobody had derived this previously (I expected to find it in a table on Wikipedia!), and then I did the derivation and ended up a lot less surprised… anyway, the equation itself:
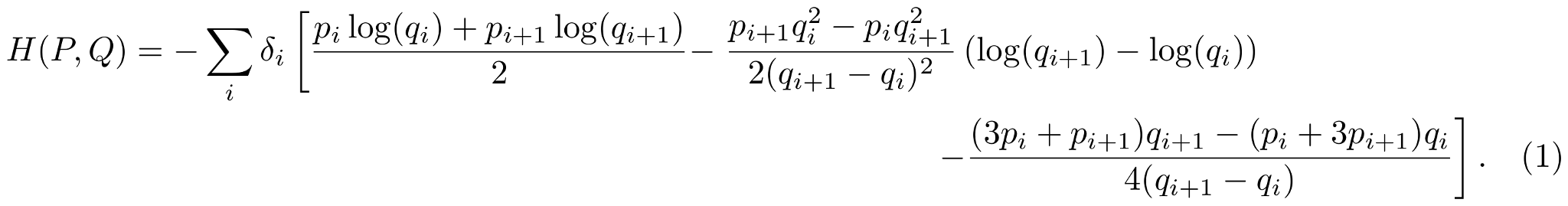
It's not the nicest result: there is a singularity when a linear segment is flat, which is not where you expect to find one for an information theoretic equation. In practice it doesn't matter (see paper), and pushing gradients through it to train a neural network is demonstrated. One thing learned from all of this is that writing "piecewise linear probability density function" many times gets annoying, and while it only just about appears in the paper I've started referring to such distributions as orograms. That is, histogram but "histo", meaning a wooden post (the bars of a histogram), has been replaced with "oro", meaning a mountain (which is what your prototypical piecewise linear PDF looks like). This is what I've called the generic library that I coded and used to generate all of the results in the paper:
Orogram — A library for working with 1D piecewise linear probability density functions
Link to OpenReview version: The Cross-entropy of Piecewise Linear Probability Density Functions by Tom S. F. Haines, TMLR, 2024.
Link to version on this web server: The Cross-entropy of Piecewise Linear Probability Density Functions by Tom S. F. Haines, TMLR, 2024.
And here's an image of the entire paper, just because it would feel weird to have nothing visual, even if it's nightmare inducing:

But that does hide just how much went into this: it's 31 pages with 218 numbered equations and an average citation year of 1982 (before I was born… just). Or, to put it more directly, the cross entropy (also, KL-divergence and entropy) of piecewise linear functions turns out to be a lot more work than you initially think it's going to be. Was surprised to discover nobody had derived this previously (I expected to find it in a table on Wikipedia!), and then I did the derivation and ended up a lot less surprised… anyway, the equation itself:
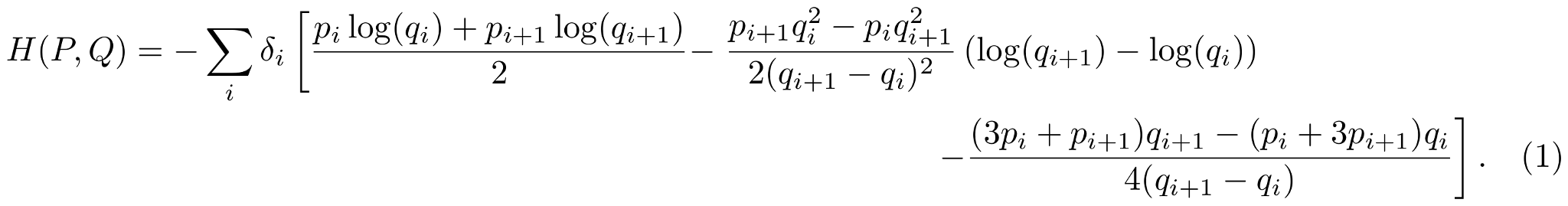
It's not the nicest result: there is a singularity when a linear segment is flat, which is not where you expect to find one for an information theoretic equation. In practice it doesn't matter (see paper), and pushing gradients through it to train a neural network is demonstrated. One thing learned from all of this is that writing "piecewise linear probability density function" many times gets annoying, and while it only just about appears in the paper I've started referring to such distributions as orograms. That is, histogram but "histo", meaning a wooden post (the bars of a histogram), has been replaced with "oro", meaning a mountain (which is what your prototypical piecewise linear PDF looks like). This is what I've called the generic library that I coded and used to generate all of the results in the paper:
Orogram — A library for working with 1D piecewise linear probability density functions
Link to OpenReview version: The Cross-entropy of Piecewise Linear Probability Density Functions by Tom S. F. Haines, TMLR, 2024.
Link to version on this web server: The Cross-entropy of Piecewise Linear Probability Density Functions by Tom S. F. Haines, TMLR, 2024.
And here's an image of the entire paper, just because it would feel weird to have nothing visual, even if it's nightmare inducing:
